box n balls rayleigh distribution The probability density function of the Rayleigh distribution is$${\displaystyle f(x;\sigma )={\frac {x}{\sigma ^{2}}}e^{-x^{2}/(2\sigma ^{2})},\quad x\geq 0,}$$ See more Tamper-resistant junction box for compact UniFi Dome and Turret cameras that enhances mounting durability, aesthetics, and ease of maintenance.
0 · rayleigh distribution wiki
1 · rayleigh distribution scale
2 · rayleigh distribution probability
3 · rayleigh distribution normal range
4 · rayleigh distribution examples
5 · rayleigh distribution chart
6 · rayleigh distribution calculation
7 · rayleigh distribution and normal distribution
learning SOLIDWORKS for creating real-world sheet metal components. This textbook is a great help for SOLIDWORKS users new to sheet metal design. It consists of total 132 pages covering the sheet metal design environment of SOLIDWORKS. It teaches users to use SOLIDWORKS mechanical design software for creating parametric 3D sheet metal .
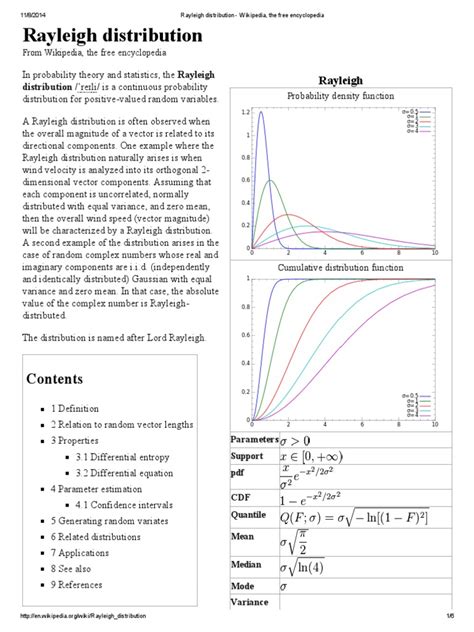
In probability theory and statistics, the Rayleigh distribution is a continuous probability distribution for nonnegative-valued random variables. Up to rescaling, it coincides with the chi distribution with two degrees of freedom. The distribution is named after Lord Rayleigh . A Rayleigh distribution is often observed when . See more
The probability density function of the Rayleigh distribution is$${\displaystyle f(x;\sigma )={\frac {x}{\sigma ^{2}}}e^{-x^{2}/(2\sigma ^{2})},\quad x\geq 0,}$$ See moreConsider the two-dimensional vector $${\displaystyle Y=(U,V)}$$ which has components that are bivariate normally distributed, centered at zero, with equal variances $${\displaystyle \sigma ^{2}}$$, and independent. Then $${\displaystyle U}$$ See moreGiven a random variate U drawn from the uniform distribution in the interval (0, 1), then the variate$${\displaystyle X=\sigma {\sqrt {-2\ln U}}\,}$$has a Rayleigh distribution with parameter See moreAn application of the estimation of σ can be found in magnetic resonance imaging (MRI). As MRI images are recorded as complex images . See more
The raw moments are given by:$${\displaystyle \mu _{j}=\sigma ^{j}2^{j/2}\,\Gamma \left(1+{\frac {j}{2}}\right),}$$where See more• $${\displaystyle R\sim \mathrm {Rayleigh} (\sigma )}$$ is Rayleigh distributed if $${\displaystyle R={\sqrt {X^{2}+Y^{2}}}}$$, . See more
rayleigh distribution wiki
• Circular error probable• Rayleigh fading• Rayleigh mixture distribution• Rice distribution See more(Thus, Dn can take any integer value between 2 and n +1.) (A) Show that for each fixed value of x > 0, n-oo (B) The continuous probability distribution with c.d.f F(x) 1-e-/2 -0 for o is called the Rayleigh distribution. The Rayleigh distribution, named for William Strutt, Lord Rayleigh, is the distribution of the magnitude of a two-dimensional random vector whose coordinates are .
B_{2010}$ and 10n $ balls have been distributed among them, for some positive integer $n$. You may redistribute the balls by a sequence of moves; each of which .What is the Rayleigh distribution? The Rayleigh distribution is a continuous probability distribution for non-negative-valued random variables — variables of 0 or higher. It is skewed right, with its maximum point occurring at a non-zero .Distributing k distinguishable balls into n distinguishable boxes, without exclusion, corresponds to forming a permutation of size k, with unrestricted repetitions, taken from a set of size n. .The Rayleigh distribution curve has the shape shown in Figure 1. For this distribution, the probability P that the absolute amplitude A has a value for A> is obtained by integrating the .
Rayleigh Distribution √Let U ∼ N(0,σ2)andV ∼ N(0,σ2) be independent random variables, define X = U2 +V2,thenX has aRayleigh distribution with the cumulative probability distribution (c.d.f.) .
We study the different properties of the Rayleigh distribution. These include the descriptive properties, reliability properties and stochastic orders.Transformation Methods: Box-Muller Algorithm I Proposition. If R2 ˘Exp(1 2) and ˘U[0;2ˇ] are independent then X= Rcos , Y = Rsin are independent with X˘N(0;1); Y ˘N(0;1): Proof: We .In probability theory and statistics, the Rayleigh distribution is a continuous probability distribution for nonnegative-valued random variables. Up to rescaling, it coincides with the chi distribution with two degrees of freedom. The distribution is named after Lord Rayleigh (/ ˈreɪli /). [1](Thus, Dn can take any integer value between 2 and n +1.) (A) Show that for each fixed value of x > 0, n-oo (B) The continuous probability distribution with c.d.f F(x) 1-e-/2 -0 for o is called the Rayleigh distribution.
The Rayleigh distribution, named for William Strutt, Lord Rayleigh, is the distribution of the magnitude of a two-dimensional random vector whose coordinates are independent, identically distributed, mean 0 normal variables. The distribution has a number of applications in settings where magnitudes of normal variables are important. B_{2010}$ and 10n $ balls have been distributed among them, for some positive integer $n$. You may redistribute the balls by a sequence of moves; each of which consists of choosing an $i$ and moving exactly $i$ balls from box $B_i$ into any one other box.
What is the Rayleigh distribution? The Rayleigh distribution is a continuous probability distribution for non-negative-valued random variables — variables of 0 or higher. It is skewed right, with its maximum point occurring at a non-zero point. The distribution is used to model the magnitude of random variables that show circular symmetry.Distributing k distinguishable balls into n distinguishable boxes, without exclusion, corresponds to forming a permutation of size k, with unrestricted repetitions, taken from a set of size n. Therefore, there are nk different ways to distribute k distinguishable balls into n distinguishable boxes, without exclusion. Case 3The Rayleigh distribution curve has the shape shown in Figure 1. For this distribution, the probability P that the absolute amplitude A has a value for A> is obtained by integrating the area under the probability density curve. Suppose your ball distribution is: $$\text{box}_1 = 2, \text{box}_2 = 0, \text{box}_3 = 1, \text{box}_4 = 0$$ You can encode this configuration in the sequence 0010$ with the $'s representing the balls and Rayleigh Distribution √Let U ∼ N(0,σ2)andV ∼ N(0,σ2) be independent random variables, define X = U2 +V2,thenX has aRayleigh distribution with the cumulative probability distribution (c.d.f.) and pprobability density function (p.d.f.) given below. F(x)=1−e−x2/2σ2,x>0 =0,x≤ 0 f(x)=x σ2 e −x2/2σ2,x>0 =0,x≤ 0 E(X)= ∞ 0 x2 .'s$ the transition from one box to the other.
We study the different properties of the Rayleigh distribution. These include the descriptive properties, reliability properties and stochastic orders.
In probability theory and statistics, the Rayleigh distribution is a continuous probability distribution for nonnegative-valued random variables. Up to rescaling, it coincides with the chi distribution with two degrees of freedom. The distribution is named after Lord Rayleigh (/ ˈreɪli /). [1](Thus, Dn can take any integer value between 2 and n +1.) (A) Show that for each fixed value of x > 0, n-oo (B) The continuous probability distribution with c.d.f F(x) 1-e-/2 -0 for o is called the Rayleigh distribution.
The Rayleigh distribution, named for William Strutt, Lord Rayleigh, is the distribution of the magnitude of a two-dimensional random vector whose coordinates are independent, identically distributed, mean 0 normal variables. The distribution has a number of applications in settings where magnitudes of normal variables are important. B_{2010}$ and 10n $ balls have been distributed among them, for some positive integer $n$. You may redistribute the balls by a sequence of moves; each of which consists of choosing an $i$ and moving exactly $i$ balls from box $B_i$ into any one other box.
What is the Rayleigh distribution? The Rayleigh distribution is a continuous probability distribution for non-negative-valued random variables — variables of 0 or higher. It is skewed right, with its maximum point occurring at a non-zero point. The distribution is used to model the magnitude of random variables that show circular symmetry.
Distributing k distinguishable balls into n distinguishable boxes, without exclusion, corresponds to forming a permutation of size k, with unrestricted repetitions, taken from a set of size n. Therefore, there are nk different ways to distribute k distinguishable balls into n distinguishable boxes, without exclusion. Case 3
The Rayleigh distribution curve has the shape shown in Figure 1. For this distribution, the probability P that the absolute amplitude A has a value for A> is obtained by integrating the area under the probability density curve. Suppose your ball distribution is: $$\text{box}_1 = 2, \text{box}_2 = 0, \text{box}_3 = 1, \text{box}_4 = 0$$ You can encode this configuration in the sequence 0010$ with the $'s representing the balls and Rayleigh Distribution √Let U ∼ N(0,σ2)andV ∼ N(0,σ2) be independent random variables, define X = U2 +V2,thenX has aRayleigh distribution with the cumulative probability distribution (c.d.f.) and pprobability density function (p.d.f.) given below. F(x)=1−e−x2/2σ2,x>0 =0,x≤ 0 f(x)=x σ2 e −x2/2σ2,x>0 =0,x≤ 0 E(X)= ∞ 0 x2 .'s$ the transition from one box to the other.

rayleigh distribution scale
Unique Metal Fabrications Inc. is a metal fabricator with capabilities to fabricate a variety of aluminum, stainless steel and other alloys. Based in Pittsburg, Kan., the company operates computer numeric control (CNC) equipment, comprising CNC beam line, CNC angle line, CNC flame cutter, press brake and CNC Whitney 661.
box n balls rayleigh distribution|rayleigh distribution probability