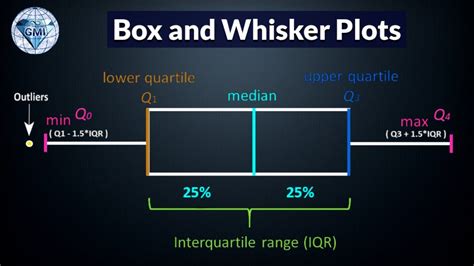
normal distribution based on box and whisker The image below shows how a box and whisker plot compares to the probability distribution function for a normal distribution. The box itself is the interquartile range, which contains 50% of your data. Additionally, notice how each whisker . Seeking a two-story barndominium floor plan? Check out our curated collection below. Two-story house designs offer homeowners a separation of spaces. Consider this: it's nighttime, and you wish to retire to your beautiful and relaxing primary suite. Do you prefer the convenience of a main-level primary suite?
0 · symmetrical box distribution
1 · right skewed distribution box
2 · how to find box distribution
3 · difference between box and whiskers
4 · box vs whisker plot
5 · box and whiskers explained
6 · box and whiskers chart
7 · box and whisker plot example
Take a look at the Lofted Flange command to generate twists in sheet metal geometry.
The image below shows how a box and whisker plot compares to the probability distribution function for a normal distribution. The box itself is the interquartile range, which contains 50% of your data. Additionally, notice how each whisker .A box plot (aka box and whisker plot) uses boxes and lines to depict the distributions of one or more groups of numeric data. Box limits indicate the range of the central 50% of the data, with .
Review of box plots, including how to create and interpret them. A boxplot, also known as a box plot, box plots, or box-and-whisker plot, is a standardized way of displaying the distribution of a data set based on its five-number summary .
Listing a Five-Number Summary and Describing the Distribution . For each box-and-whisker plot, list the five-number summary and describe the distribution based on the location of the median. a. Minimum value →4. .Box plots are non-parametric: they display variation in samples of a statistical population without making any assumptions of the underlying statistical distribution [3] (though Tukey's boxplot assumes symmetry for the whiskers .
The box and whisker plot gives us a visual of how data is distributed. The “box” represents the interquartile range, indicating where the middle fifty percent of the data lies. On either end of the box, you’ll find the first (lower) quartile (the 25% .A box plot, also known as a box-and-whisker plot, is a standardized way of displaying the distribution of data based on a five-number summary: minimum, first quartile (Q1), median, third quartile (Q3), and maximum.
How to read Box and Whisker Plots. Box and whisker plots portray the distribution of your data, outliers, and the median. The box within the chart displays where around 50 percent of the data points fall. It summarizes a data set in five .
A box and whisker plot is determined from the _____, the smallest and the largest values, and the lower and upper quartile. . A _____ distribution is similar to a normal distribution but has a lower peak and fatter tails. mesokurtic. If the mean of a distribution is greater than the median, then the distribution is _____. Method 1 – Create Box and Whisker Plot Using Box and Whisker Chart. Select the range of cells from B4 to E13. Go to the Insert tab in the ribbon. Select the Insert Statistic Chart drop-down option from the Charts group. . Here, the Whisker end-points are based on the 1.5 IQR rule (used to identify outliers in the dataset) Outliers: Identifying the Extremes. Outliers, the extreme values in a dataset, are plotted as . We can determine whether or not a distribution is skewed based on the location of the median value in the box plot. When the median is closer to the bottom of the box and the whisker is shorter on the lower end of the box, the distribution is right .
I am trying to know if the below box-plot represents a normal distribution or if its similar to a normal but i have some doubts about it. The median is 2.0, mean is 2.5 and sd is 1.60. Although the box is symmetric the lengths of whisker are not also mean is not equal to median so i would say this is not similar to a gaussian distribution but i .

x act sheet metal inc
symmetrical box distribution

It has a different use. Normally I'd overlay a normal distribution on a histogram. A box plot can be used to compare data that aren't normally distributed. The intent behind box plots is to get an idea of where most of the data are and visualize if some data are quite far away, depending on how the whiskers are determined.statistics based on the normal distribution (Massart et al. 2005). b. Comparing box and whisker plots and quantifying data differences Another advantage of the box and whisker plot is the ability to compare multiple datasets side-by-side, as idealized in Figure 3. Important characteristics of
There might be two outliers in distribution A, based on R’s definition 8. Box plots are a powerful way to see how data is spread out, making them essential for analyzing and understanding data. Box Plots and Whisker Diagrams: Visualizing Data Distribution. Box plots, also known as box-and-whisker diagrams, are great for showing how data is .*Thirty or more is typically regards as a large enough sample size for any distribution to be treated like a normal distribution *According to the central limit theorem, the sampling distribution of the mean approaches a normal distribution as sample size increase *You can confidently estimate a population mean from sample data of 35 measurements, even if the underlying distribution is . Interpretation of Box and Whisker Plot. Normal Distribution or Symmetric Distribution: If a box plot has equal proportions around the median and the whiskers are the same on both sides of the box then the distribution is normal. Positively Skewed: A distribution is positively skewed when the median is closer to the bottom quartile (Q1).
Download scientific diagram | Example of a box-and-whisker plot for a normal distribution. Classification intervals marked by the coloured boxes red, orange and green. from publication: Outcomes .
A stats component of a boxplot object "contains the extreme of the lower whisker, the lower hinge, the median, the upper hinge and the extreme of the upper whisker"; the first and last of those are the cutoffs for outliers as you defined them.* With 1000 values and a hoped-for 1% outliers, you would get about 10.As @whuber comments, you should apply that rule on the scale used to draw the box plots. If a transformation seems natural or appropriate, calculations should be on that scale. Above all, don't mix scales (e.g. calculate whiskers based on 1.5 IQR on the raw scale, then log transform to get a new graph). $\endgroup$ – This has been well answered. These extra comments are a little too long (UPDATE: now a lot too long) to go as comments. Strictly, all you can read off a boxplot about the variability of a distribution are its interquartile range (the length or height of the box) and range (the length or height between the extremes of the display).
In box plot for normal distribution, the median of the distribution is in the middle of the box, and the whiskers are about the same on both sides of the box. whereas for Positively or Right .View Module 2 Assignment.xlsx from PHA 6935 at University of Florida. PHA6935 Megan S. 1. Explain the following terms in your own words. a. Box-and-whiskers plot - A box and whisker plot consists of
Box‐and‐Whisker Plot . following standard normal distribution • Calculate median, first, and third quartiles • Calculate IQR and find ranges shown below • Find and count left and right outliers • Do not use built‐in Matlab functions for this! . How good is the model based on a particular .
Box‐and‐Whisker Plot . following standard normal distribution • Calculate median, first, and third quartiles • Calculate IQR and find ranges shown below • Find and count left and right outliers • Do not use built‐in Matlab functions for this! . How good is the model based on a particular . Histograms and Box plots show the distribution of three datasets. Image by author. The problem can be simply explained: Box plots lack showing the mode(s) of a dataset. Besides, being defined as the value that occurs most often, mode(s) also refers to the local maximum of a distribution. When coping with a bimodal distribution, which has two modes (or peaks), or .
right skewed distribution box
Study with Quizlet and memorize flashcards containing terms like The _____ is a graphic that is used to visually check whether data come from a normal population Exponential plot normal probability plot box and whiskers plot normal distribution graph, It is appropriate to use the uniform distribution to describe a continuous random variable x when the area under the probability . This leads to many outliers, because the maximum whisker length is computed as a multiple (default: 1.5) of the interquartile range (the box height), which does not scale across orders of magnitude. Alternatively, you could specify to draw the whiskers for a given percentile range: ax.boxplot(values, whis=[5, 95]) In this case you get a fixed .Common alternative whisker positions include the 9th and 91st percentiles, or the 2nd and 98th percentiles. These are based on the properties of the normal distribution, relative to the three central quartiles. Under the normal distribution, the distance between the 9th and 25th (or 91st and 75th) percentiles should be about the same size as .
$\begingroup$ @NickCox thanks; actually, I'd have guessed heights wouldn't be bimodal; imagine that (as a rough approximation to reality) we considered two normal distributions with similar standard deviations, whose means differ by about 1sd, with about as many males as females. Then in fact the combined (mixture of two normals) distribution .The two vertical lines (called whiskers) outside the box extend to the smallest and largest observations within 1.5 x IQR (interquartile range) of the quartiles. If there are no outliers, then the whiskers extend to the min and . each from an underlying normal distribution. H 1: The means are the two samples (or treatments) are different. H 0How to read Box and Whisker Plots. Box and whisker plots portray the distribution of your data, outliers, and the median. The box within the chart displays where around 50 percent of the data points fall. It summarizes a data set in five marks. The mark with the greatest value is called the maximum. It will likely fall far outside the box. $\begingroup$ It's a relatively simple multiple and it results in an expected outlier rate of just under 1% for Normal distributions. If it were changed to 2.0, the rate would drop to 0.07% and if it were set only at 1.0, the rate would soar to over 4%. Since Tukey used boxplots to analyze smallish batches of data (comprising five to a few hundred values), a rate of 1% would .
Data drawn from a normal distribution will typically have somewhere between a small and a substantial proportion of points outside the whiskers. e.g. in samples of size 9 from an exactly normal distribution, more than 30% of the time you'll see at least one value outside the whiskers
xlr cable junction box
Junction boxes protect electrical wires from damage, prevent shocks, and stop sparks from igniting flammable material nearby. To install one, you’ll need to strip the ends off all the wires that will be in the box. To .
normal distribution based on box and whisker|right skewed distribution box