comparing the distribution of box plots Box plot is a graphical representation of the distribution of a dataset. It displays key summary statistics such as the median, quartiles, and potential outliers in a concise and visual manner. By using Box plot you can .
$299.00
0 · side by boxplot interpretation
1 · matlab boxplot vs box chart
2 · how to solve box plots
3 · comparing box plots worksheet pdf
4 · comparing box plots worksheet
5 · comparing box plots problems
6 · comparing box plots and histograms
7 · comparing box and whisker plots
All UWS truck tool boxes feature a patented* RigidCore lid, extra-thick aluminum construction and stainless steel lock handles. They are available in several different sizes, styles and finishes to perfectly suit each unique pickup truck bed.
When comparing two or more box plots, we can answer four different questions: 1. How do the median values compare? We can compare the vertical line in each box to determine which dataset has a higher median .Box plots are a useful way to compare two or more sets of data visually. In statistics, a box plot is used to provide a visual summary of data. The distribution of data is shown through the .A box plot, sometimes called a box and whisker plot, provides a snapshot of your continuous variable’s distribution. They particularly excel at comparing the distributions of groups within your dataset.
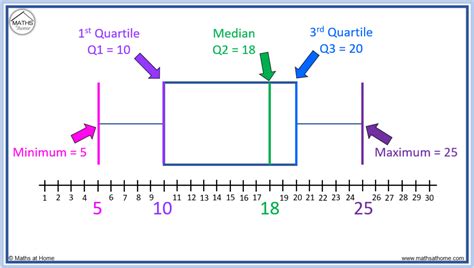
Box plots visually show the distribution of numerical data and skewness by displaying the data quartiles (or percentiles) and averages. Box plots show the five-number summary of a set of data: including the minimum . This post describes box plots and shows their advantages. Box plots, also called box and whisker plots, are more useful than histograms for comparing distributions. Box plot is a graphical representation of the distribution of a dataset. It displays key summary statistics such as the median, quartiles, and potential outliers in a concise and visual manner. By using Box plot you can . Box plots are useful because they allow us to gain a quick understanding of the distribution of values in a dataset. They’re also useful for comparing two different datasets. When comparing two or more box plots, we .
When comparing two or more box plots, we can answer four different questions: 1. How do the median values compare? We can compare the vertical line in each box to determine which dataset has a higher median .We can compare two box plots numerically according to their centers, or medians, and their spreads, or variability. Range and interquartile range (IQR) are both measures of spread. Box . When comparing two or more box plots, we can answer four different questions: 1. How do the median values compare? We can compare the vertical line in each box to determine which dataset has a higher median value. 2. How does the dispersion compare?In this explainer, we will learn how to compare two data set distributions using box plots. Box plots, which are sometimes called box-and-whisker plots, can be a good way to visualize differences among groups that have been measured on the same variable.
Box plots are a useful way to compare two or more sets of data visually. In statistics, a box plot is used to provide a visual summary of data. The distribution of data is shown through the positions of the median and the quartiles.A box plot, sometimes called a box and whisker plot, provides a snapshot of your continuous variable’s distribution. They particularly excel at comparing the distributions of groups within your dataset.
Box plots visually show the distribution of numerical data and skewness by displaying the data quartiles (or percentiles) and averages. Box plots show the five-number summary of a set of data: including the minimum score, first (lower) quartile, median, third (upper) quartile, and maximum score. This post describes box plots and shows their advantages. Box plots, also called box and whisker plots, are more useful than histograms for comparing distributions. Box plot is a graphical representation of the distribution of a dataset. It displays key summary statistics such as the median, quartiles, and potential outliers in a concise and visual manner. By using Box plot you can provide a summary of the distribution, identify potential and compare different datasets in a compact and visual manner.
Box plots are useful because they allow us to gain a quick understanding of the distribution of values in a dataset. They’re also useful for comparing two different datasets. When comparing two or more box plots, we can answer four different questions: 1. How do the median values compare? When comparing two or more box plots, we can answer four different questions: 1. How do the median values compare? We can compare the vertical line in each box to determine which dataset has a higher median value. 2. How does the dispersion compare?We can compare two box plots numerically according to their centers, or medians, and their spreads, or variability. Range and interquartile range (IQR) are both measures of spread. Box plots with similar variability should have similar boxes and whiskers.
When comparing two or more box plots, we can answer four different questions: 1. How do the median values compare? We can compare the vertical line in each box to determine which dataset has a higher median value. 2. How does the dispersion compare?
In this explainer, we will learn how to compare two data set distributions using box plots. Box plots, which are sometimes called box-and-whisker plots, can be a good way to visualize differences among groups that have been measured on the same variable.Box plots are a useful way to compare two or more sets of data visually. In statistics, a box plot is used to provide a visual summary of data. The distribution of data is shown through the positions of the median and the quartiles.
A box plot, sometimes called a box and whisker plot, provides a snapshot of your continuous variable’s distribution. They particularly excel at comparing the distributions of groups within your dataset.
Box plots visually show the distribution of numerical data and skewness by displaying the data quartiles (or percentiles) and averages. Box plots show the five-number summary of a set of data: including the minimum score, first (lower) quartile, median, third (upper) quartile, and maximum score. This post describes box plots and shows their advantages. Box plots, also called box and whisker plots, are more useful than histograms for comparing distributions. Box plot is a graphical representation of the distribution of a dataset. It displays key summary statistics such as the median, quartiles, and potential outliers in a concise and visual manner. By using Box plot you can provide a summary of the distribution, identify potential and compare different datasets in a compact and visual manner.
24 sheet metal folding tool
Box plots are useful because they allow us to gain a quick understanding of the distribution of values in a dataset. They’re also useful for comparing two different datasets. When comparing two or more box plots, we can answer four different questions: 1. How do the median values compare? When comparing two or more box plots, we can answer four different questions: 1. How do the median values compare? We can compare the vertical line in each box to determine which dataset has a higher median value. 2. How does the dispersion compare?
side by boxplot interpretation
matlab boxplot vs box chart
The Fabricated Metal Products Manufacturing Industry is comprised of multiple sub-industries, from Structural Metal Product Manufacturing to Ball Bearing Manufacturing. The 15 sub-industries have a total market size of $390Bn and a compound annual growth rate (CAGR) of 2.3% for the five years ending 2021.
comparing the distribution of box plots|comparing box plots problems